信息学院王浩课题组与合作者在非凸优化算法研究中取得重要进展,提出了一种求解非凸Lp范数球投影问题的高效算法。相关成果以“Towards an Efficient Approach for the Nonconvex Lp-ball Projection: Algorithm and Analysis”为题，被理论机器学习领域知名学术期刊 Journal of Machine Learning Research (JMLR)接收。
稀疏性已经成为现代数据科学和工程领域中表征感兴趣的参数和信号的基本结构之一。 稀疏性能自然地体现具有少数非零元的$n$-维信号的紧凑模式, 使得信号能够被少于$n$个数据比特的有效信息表示。例如, 在许多机器学习问题中, 稀疏解克服了欠定线性系统的不适定性, 增强了具有大量冗余特征模型的可解释性, 提高了学习系统的泛化性能, 并保证了模型在训练和推理阶段都显著地节省计算量。稀疏性通常是通过施加可以诱导稀疏结构的正则项实现, 由此产生的非凸稀疏优化问题则对数值优化算法提出了更高的要求。
为了系统地促进模型解的稀疏性，优化与机器学习社区研究者们对非凸Lp范数球投影问题开展了大量研究。然而，Lp范数非凸、非光滑以及非利普希茨数学性质对算法的分析与设计提出了挑战，而且在大规模优化问题中，计算该投影的高效数值算法也十分有限。为此，研究团队首先推导出表征该问题最优解的一阶必要条件，继而设计了一种迭代重加权L1球投影 (Iteratively Reweighted L1 Ball Projection, IRBP) 算法计算一阶驻点的数值方法。该算法实现简单, 且计算效率高 (图1和图2)。同时，研究团队也证明了所提算法的全局收敛性以及收敛速率。该算法的提出为求解一类难以处理的稀疏约束优化问题提供了坚实的研究基础。
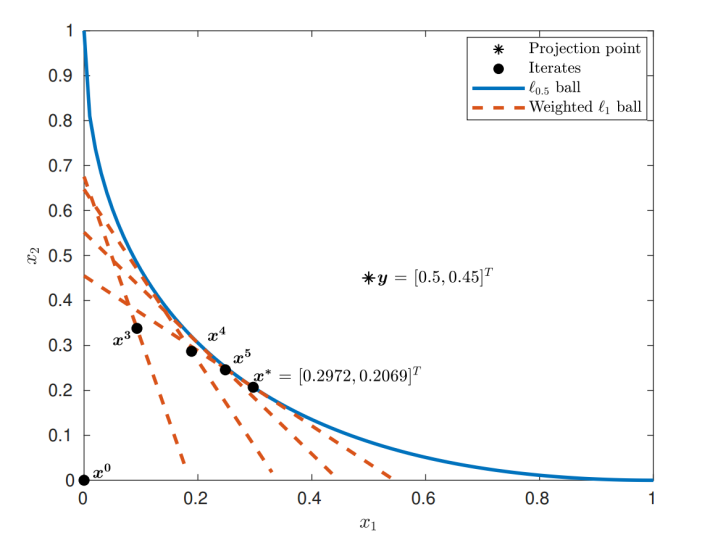
图1 IRBP求解二维L0.5范数球投影问题产生的迭代序列路径
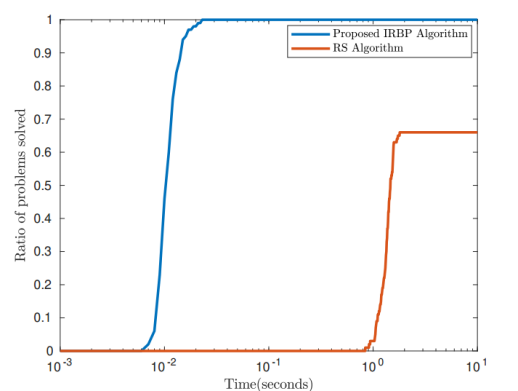
(a) p = 0.4 (b) p = 0.5
图2 IRBP与当前先进算法的性能比较
此项研究由上海科技大学、华盛顿大学等单位合作完成, 上海科技大学为第一完成单位。信息学院2019级博士生杨翔宇为第一作者, 王浩教授为通讯作者。
文章链接：https://arxiv.org/abs/2101.01350
沪公网安备 31011502006855号
