In the past two years, two novel model reduction methods for high-dimensional stochastic computational models were proposed by the Visual and Data Intelligence Center (VDI Center) of SIST. The first method, proposed in the article entitled “Rank adaptive tensor recovery-based model reduction for partial differential equations with high-dimensional random inputs”, provided a new systematic computational approach for a major problem in data science, which was to recover high order tensors without ranks given a priori. The other one, published in the article entitled “ANOVA Gaussian process modeling for high-dimensional stochastic computational models”, provided a novel analysis of variance-based model reduction approaches for Gaussian process regression, which gave efficient and reliable surrogates for complex computational models. These two articles were successively published in the top journal Journal of Computational Physics.
In the first article, a systematic model reduction approach based on rank adaptive tensor recovery was developed for partial differential equation (PDE) models with high-dimensional random parameters. Since the standard outputs of interest of these models are discrete solutions on given physical grids which are high-dimensional, kernel principal component analysis is applied to construct stochastic collocation approximations in reduced dimensional spaces of the outputs. To address the issue of high-dimensional random inputs, a new efficient rank adaptive tensor recovery approach was developed to compute the collocation coefficients. Novel efficient initialization strategies for non-convex optimization problems involved in tensor recovery were also developed in this work. A general mathematical framework of the overall model reduction approach was presented. Its stability was analyzed, and its efficiency was demonstrated with numerical experiments (see Fig 1). This work was undertaken at the School of Information Science and Technology, ShanghaiTech University. PhD student Tang Kejun is the first author. Professor Liao Qifeng is the corresponding author. This work was supported by the National Natural Science Foundation of China.
Read more at:https://www.sciencedirect.com/science/article/pii/S002199911930467X
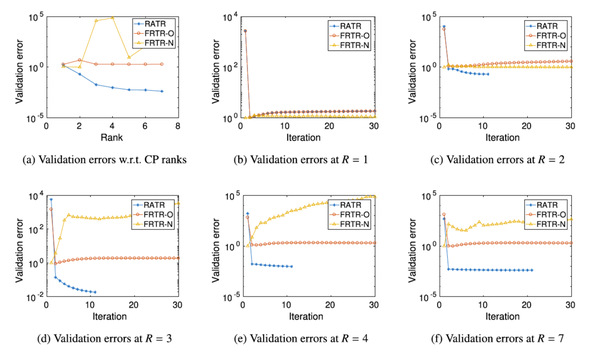
Figure 1. Validation errors of rank adaptive tensor recovery
The second article presented a novel analysis of variance Gaussian process (ANOVA-GP) emulator for models governed by partial differential equations (PDEs) with high-dimensional random inputs. The Gaussian process (GP) is a widely used surrogate modeling strategy, but it can become invalid when the inputs are high-dimensional. In this new ANOVA-GP strategy, high-dimensional inputs were decomposed into unions of local low-dimensional inputs, and principal component analysis (PCA) was applied to provide dimension reduction for each ANOVA term. Local GP models for PCA coefficients based on ANOVA decomposition were systematically built to provide an emulator for the overall high-dimensional problem. Solid numerical experiments were conducted to demonstrate the efficiency of ANOVA-GP (see Fig 2). This work was undertaken at the School of Information Science and Technology, ShanghaiTech University. Master student Chen Chen is the first author. Professor Liao Qifeng is the corresponding author. This work was supported by the National Natural Science Foundation of China.
Read more at: https://www.sciencedirect.com/science/article/pii/S0021999120301005
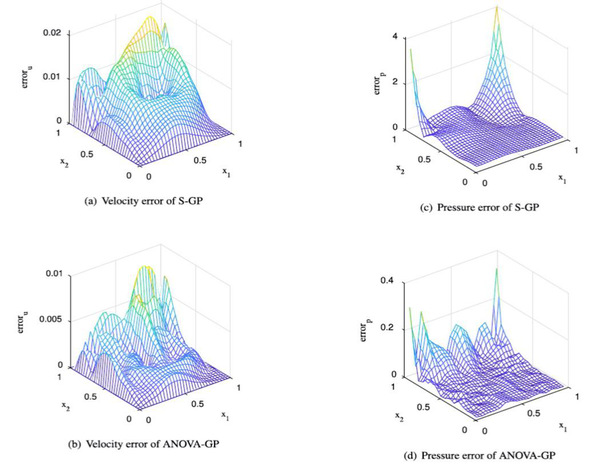
Figure 2. Errors of standard GP and ANOVA-GP




 沪公网安备 31011502006855号
沪公网安备 31011502006855号


